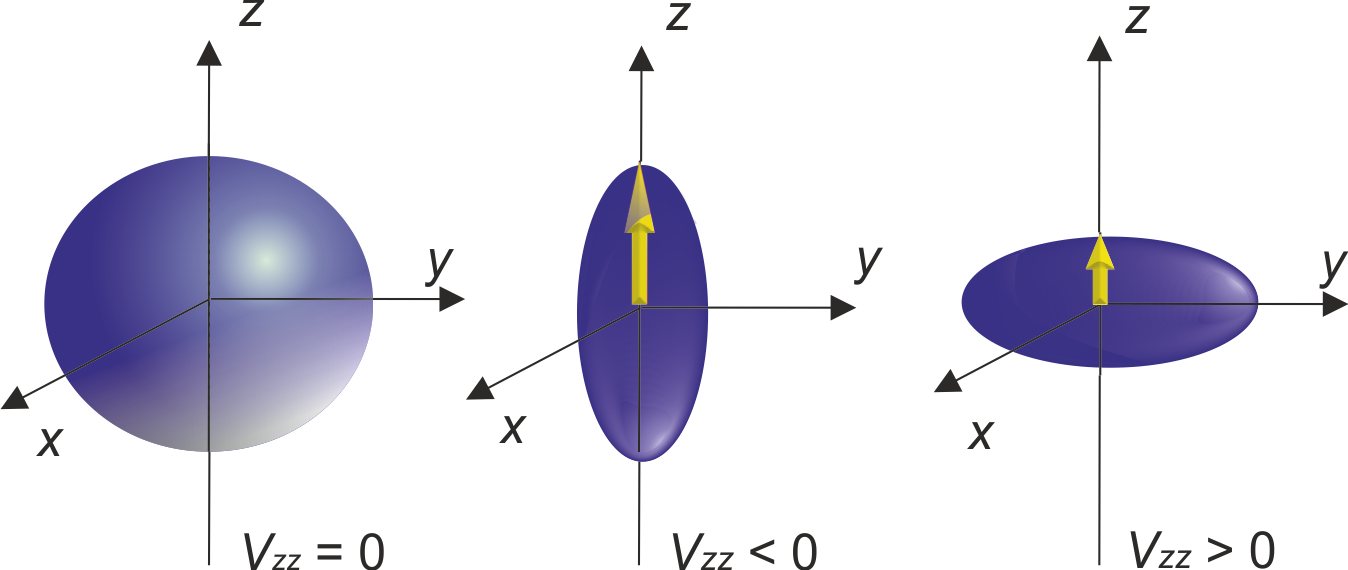
Electric Field Gradient (EFG) is a ground state property of solids, defined as the second derivative of the electrostatic potential at the nucleus position, written as a traceless tensor. It is greatly sensitive to charge distribution in the vicinity of the observed nucleus, as well as the nearest neighbour distance and their distribution! This makes it a powerful tool for electron density investigation, a physical quantity that is a direct consequence of the chemical composition of the material.
When nuclear spin (I) is larger then 1 then the nucleus in question has nuclear quadruple moment (Q) that differs from zero, i.e. nuclear charge is not spherically distributed. Such nucleus, or more precise, nuclear quadrupole moment can interact with the electric field gradient surrounding the nucleus. This interaction determines nuclear quadrupole frequency (ν_Q) and asymmetry parameter (η_Q).

Experimental techniques by which the EFG can be studied are:
nuclear quadrupole resonance (NQR),
nuclear magnetic resonance (NMR),
Mössbauer spectroscopy,
the time differential perturbed angular correlation (TDPAC).

Part of our group that deals with hyperfine interactions by performing experiments use TDPAC and Mössbauer apparatus . Their measurements are supported with Ab Initio calculations of the structure, electronic and hyperfine properties of the investigated materials. In some of the TDPAC measurements, calculations are necessity! The interpretation of the results gained with this experimental method can be complicated, due to the fact that the site of the probe atom used can be unknown. By calculating hyperfine parameters and comparing them with the measured ones it can be established where did the used probe atom (Impurity) go. DFT calculations also provide a sign of EFG tensor eigenvalues and orientation of EFG axes in the crystal.

Total EFG can be decomposed into “lattice” and “valence” contribution. “Lattice contribution” originates from the charge outside the atomic sphere, while the valence contribution arises from the charge within. Electrons are distributed within the atomic orbitals, which can be completely occupied, partially occupied or empty. Now, “valence EFG” can be decomposed into partial wave functions, p-p, s-d, d-d, p-f and f-f, and this decomposition corresponds to the occupation of orbitals. The distribution of electronic charge within the atomic sphere dominates the EFG when compared to lattice contribution, which is usually very small.

Information on the values and the signs EFGs combined with the knowledge of the density of states and electron density plots can be used for the better understanding of electronic charge distribution and chemical bonding type in crystals. Ionic crystals, for example, can have electronic charge closely distributed or well depleted around nucleus.

In short, investigation of hyperfine structure of nuclei can explain the interactions of atomic nucleus with local electric fields, by which knowledge of symmetry of charge distribution around nucleus, electronic configurations of atoms and peculiarities of atomic structure of solids could be induced.

Effect of the interstitial hydrogen on electric field gradient (IH/EFG)

Insertion of the hydrogen atoms in the interstitial positions of these materials, has been proven to alter the local electric fields in the nearest neighbours of hydrogen, as well as the magnetic moments of magnetic materials. This is followed by the modification in electronic distribution and consequently change in chemical bonding between atoms. Considering that in Laves phases hydrogen can be found in different interstitial sites and that it is surrounded by different parent atoms in all those sites, bonding properties are different in every hydrogen configuration. The idea of IH/EFG studies is to show the change or lack of it in the gradient of electric fields and other hyperfine interactions when hydrogen is found in the crystal cell in all its configurations. Also, to establish the connection within the charge transfer, chemical bonding and the hyperfine interactions in mentioned intermetallics. When these connections are once established it could enable the easier predictions of Laves phases behaviour when hydrogen storage is in question.